
Abstract
Deep Implicit Surface는 generic shape에 대해서 탁월한 Reconstruction을 보여주었지만, Manufactured objects에 대해서 그 형상을 잘 표현해내지는 못했습니다. 본 논문은 Explicit한 파라미터와 Latent code로 이 문제를 극복하고자 합니다. 이러한 방법론은 3D Shapes을 효율적으로 조절하게 도와줍니다.
1. Introduction
SDF 표현방법의 장점 명확하지만, 단점 또한 명확합니다. 형상을 학습하기는 하지만, 임의로 학습하기 때문에 몇 개의 Parameters로 표현할 수 있는 간단한 형상 등을 표현하는데 어려움을 겪습니다. 예를 들어, 자동차의 전체 형상은 잘 학습할지 몰라도, 자동차의 타이어나 휠 부분을 학습하는 것은 사실상 불가능합니다.
이를 극복하고자 본 연구는 geometric primitives와 generic surfaces를 결합한 독창적인 Implicit Representation 방법론을 제시합니다. 이는 Parametric Manipulation 을 가능케 합니다. 본 논문은 세 가지의 Primitives를 정의합니다.
1. Generic primitives: 임의의 SDF로 표현된 복잡한 형상
2. Simple geometric primitives: 구나 원통 등으로 표현할 수 있는 간단한 형상
3. Pseudo-Primitives: 간단한 형상과 굉장히 비슷하나 엄연히 다른 형상(자동차 휠)
이러한 세 가지 Primitives를 정의하고자, Generic-SDF, Geometric-SDF과 Geometry-assisted-SDF를 각각 제시합니다. 이것들은 implicit latent vectors와 Explicit Geometric Parameters로 Parametrized됩니다.

이러한 접근은 3D Models을 해석 가능하게 합니다. 요약하자면, CAD에 포함되는 다양한 다른 종류의 Primitives를 합해 이것들을 해석 가능케 하는 것은 물론이고 수정도 일관적으로 가능케 합니다. 이는 사용자에게 있어 user-friendly 3D Shape Manipulation을 가능케 하고 자동으로 Parameter Detection이 가능합니다.
2. Related Works
2.1 Primitive based Representations
기존 Primitive-Based 방법론은 3D Shape을 의미있게 Semantic Segmentation하는데 초점을 두었다. 모든 연굿들은 simple한 Primitives를 가지고 학습을 하였으며, Reconstruction Accuracy는 Primitives에 따라 달라지는 경향이 있었다.
2.2 Explicit and Implicit Surfaces
3D surface 표현 방식 중에 mesh는 가장 널리 활용되는 방식이다. 메쉬는 Known Shape에 대해서는 Refine도 가능하지만, Unknown Shape에 대해서는 거의 어떤 것도 생성하는 것이 불가능하다. 이전에도 메쉬를 통해 3D Mesh를 생성하려는 시도가 있었으나 일반화하는데 큰 어려움이 있었다.
이에 대한 대안으로 Implicit Representation이 주목받는데 Volumetric Function을 통해 형상을 표현하는 방식이다. 이러한 방식의 최고 강점은 위상을 쉽게 바꿀 수 있다는 점이다. 이전에는 Volume단위에서 이것들을 표현하는 것이기 때문에 굉장히 Computation Cost가 많이 든다고 여겨졌지만, 현재는 Deep Implicit-fields의 탄생으로 그 변화가 극적으로 일어났다.
2.3 Hybrid Representation
Hybrid Methods는 다른 표현방식을 하나로 묶는 것이다. 가장 주로 쓰이는 방법은 points, voxels 등의 다른 방법론들을 Shared Latent Vectors를 사용해 Classification 혹은 Segmentation을 강화하는 것이다. 하지만 DualSDF만이 Shape Generation과 Manipulation을 가능케 하는 Hybrid Representation 방법론이다. 여러 장점이 있는 모델이지만, Primitives의 표현력에는 어려움이 있고 Semantically meaningful parts에 대응하지 못한다는 단점이 있다.
3. Approach
본 문제에 대한 접근 방법은 다음과 같다. 먼저 latent vectors과 Geometric Parameters를 Decoding해 3D Shapes를 표현한다. 그리고 Loss를 토대로 학습한다.

3.1 HybridSDF Representation

$SDF_{prim}(P)$은 미분가능한 Volumetric Function으로 $S_{prim}$은 shape을 표현한다. 이것들은 Explicit하게 혹은 Implicit하게 표현할 수 있다. 추가적으로 Rotation과 Translation에 대한 Parameter도 정의한다. 이는 6D Pose를 표현할 수 있는 방식이다. 기존 p를 아래와 같은 방식으로 변환할 수 있다.

Generic SDF: 임의의 복잡한 형상을 의미한다. 이는 Latent Vectors 혹은 Explicit Parameters로 표현된다. 다만, Generic SDF는 Rotation이나 Translation에 대한 파라미터는 학습하지 않는다.
Geometric-SDF: 단순한 기하학 형상은 small parameters로 표현될 수 있다. 예를 들어, Sphere 형상은 $Ψsphere(S, p) = ||p|| − r$로 표현이 될수 있다.
Geometric-assisted-SDF: 본 논문의 가장 큰 Novelty부분이라고 볼 수 있다. 기계장치같은 경우는 사실 원통이나 구와 상당히 유사하나 다른 경우가 있다. 이를 보완하기 위한 Primitives로 $SDF_{assist}(P)$로 표현할 수 있다. $S_{a} = (LV_{assist}, S_{assist})$로 표현한다. 추가적으로 이는 이를 assist하는 일반 기하학 형상과 가깝도록 constrain을 걸어준다. 이를 위해서 $SDF_{assist}(p) ≈ SDF_{geom}(p)$가 되도록 학습한다.
결국에는 Full Shape은 모든 Primitives의 합으로 취해진다. 따라서 이러한 SDF는 직접적으로 모든 SDFs min Operator를 적용해 직접적으로 만들 수 있다. 이는 구조적 입체기하학에서 그 개념을 가지고 왔다. 간단히 설명하자면, 복잡한 모델을 다양한 단순한 Object들을 조합해 만드는 것이다. 본 논문은 CSG를 해당 논문(https://lightbits.github.io/papers/haugo2017continuous.pdf)을 인용하면서 설명하고 있다.


3.2 Network
형상은 vector로부터 Decoding된다. 그러나 본 논문은 Implicit과 Explicit한 표현방법이 혼재되어있다. 이는 Parameter Space에서 구분되는 Manipulation을 가능케 한다. 본 모델은 Point Cloud Encoder를 활용해 이것이 Geometric인지, Geometric-Assisted Primitives인지 구문한다. 그리고 Generic 부분의 Latent Vector는 auto decoder의 방식으로 학습된다. (한번에 Auto-Decoder로 학습하는 방식은 Appendix D를 참조하면 된다.)
우선 Latent Vector $LV_{generic}$과 S,R,T를 통해 Generic Decoder를 학습한다. 그리고 보조 아웃풋인 $SDF_{geom}$을 추가해 모든 Geometric Primitives를 예측하도록 한다. 이는 Geometric Primitives와 Genenric Primitives 사이에 일치성을 보장하기 위한 방법이다.
그다음 $SDF_{assist}$는 geometry-assisted primitives를 Part Decoder Network를 통해 디코딩한다. 이것의 Input은 $LV_{assist}$와 Shape Parameter S이다. R과 T는 position을 변경할 때 사용된다.
Point Encoder
Point Encoder의 구조는 PointNet과 상당히 유사하다. FCL로 구성되어 있고 ReLU가 적용되었다. 본 연구진은 Point Encoder의 필요성을 강조했는데 이는 Auto-Decoding Framwork에서 이러한 Parameters를 직접적으로 학습할 때에는 오로지 한번 이들 Parameters가 업데이트되기 때문이다. 이는 초기에 Local Minima로 빨리 수렴될 수 있다. 이는 Appendix C.4를 참조하면 된다.
학습하는 동안 Point Encoder는 S,R,T에 대한 값을 제공하며, Assisted Latent Vector 또한 제공한다.
3.3 Training Loss
Reconstruction Loss
직관적인 Loss Term을 사용한다.

Parts에 대해서는 만약 자동으로 생성된 것이라면 Label값이 무의미할 수 있다. 새로운 Part Reconstruction Loss Term을 소개한다. $SDF_{part}$는 Geometric 혹은 Geometry-assisted-SDF로 Part에 대응한다. Sort는 Samples을 값이 증가하는 방향으로 정렬한 것이다. K'는 K보다 작은 숫자를 의미한다.($K' = γK$) 즉, 가장 에러가 작은 몇 개에 대해서만 확인을 한다는 것이다. $γ$는 Robustness for reconstruction fidelity에 대한 트레이드 오프 하이퍼 파라미터이다. 노이즈가 더 클수록, $γ$는 더 작게 세팅되어야 한다. 만약 Part Labels이 없다면 아래 Loss Term은 0으로 둔다.

Geometry Assistance
Geometry-assisted Primitives는 그에 해당하는 Geometry를 닮아가도록 학습한다.

Intersection Loss
Primitives를 Overlapping으로 부터 막기 위해 모든 쌍에 대해서 Intersection Loss를 도입한다.

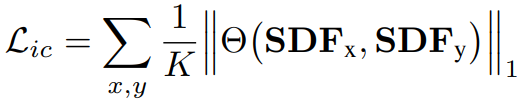
Consistency Loss
Generic Decoder를 강화하기 위해 Generic Decoder에서 나온 $SDF_{geom}$과 실제 Analytic SDF Function의 일치도에 대한 Loss Term을 둔다.이는 Generic Decoder가 Geometric Parameter에 Dependent하게 학습하기 위해 꼭 필요한 Term이다.

Regularization Loss
마지막으로 우리는 L2_Regularization을 통해 Latent Vector를 정규화했다.
5. Conclusion
Deep Implicit Surface와 Geometry Primitives를 결합한 방법론을 제시했다. 이는 정확도를 보존하며, 해석 가능성을 열어두었고 복잡한 Objects에 대해서도 일관성이 있는 Consistency를 이끌어낼 수 있었다. 이러한 구분되는 표현(Disentangled Representation)은 Geometric Parameters를 정의하기 용이하다.
Paper
https://arxiv.org/pdf/2109.10767.pdf



