Optimization Method- (2)

 이전 포스팅에서 Analytical하면서 Constraints을 가지고 있는 Optimization 문제를 어떻게 처리하는지 살펴보았다. 이번에는 Numerical 하면서 Constraints을 가지고 있는 문제들을 어떻게 처리하는지 살펴볼 예정이다. 대표적으로는 GRG와 SQP가 있는데 이번 포스팅을 통해 GRG와 함께 GRG의 한계를 보완해주는 Strategy와 Method를 집중적으로 소개할 예정이다.

 

GRG(Generalized Reduced Gradient)

- Reduced Gradient와 차이점: GRG는 Iterative Algorithm인 반면, Reduced Gradient는 Analytical Method라고 볼 수 있다.

GRG Concept

Algorithm 구성

Step 1) Gradient Descent Method와 비슷하게 decision variable 을 아래와 같은 방식으로 업데이트한다.

alpha값은 Learning Rate로 Step의 크기를 결정한다.

Step 2) State Variable을 조정한다. ($dh = 0$입니다.) Reduced Gradient에서 유도한 식을 바탕으로 아래와 같이 식을 정리할 수 있습니다.

Step 3) 아래에 서술한 식은 제약조건들을 Linearization해 풀이한 식이다. 따라서 제약조건들이 Linear하지 않다면, 정확히 맞아떨어진다고 볼 수는 없다. 하지만 $s'_(k+1)$초기 추정값을 가지고 Iterative하면 $h(d_(k+1), s_(k+1)) = 0$을 만족하는 Nonlinear System의 솔루션을 획득할 수 있다.

j는 Iteration하는 과정

위 식을 계속 반복하고 획득한 수렴값을 바탕으로 Feasible Point를 업테이트한다.

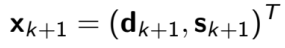
요약: step1을 통해 $d_(k+1)$값을 획득한다. Step2를 통해 $s'_(k+1)$값을 획득할 수 있다. 이는 fixed state variable값이 아니라 초기값을 획득하는 것에 불과하다. 보다 정확한 State Variable을 획득하기 위해 Step3에서 여러 번 Iteration을 실시한다. 적절한 $s_(k+1)$값을 획득한 후, Feasible Point를 업데이트하면 한 term이 마무리되고 더 나은 값을 얻기 위해 step1으로 돌아가 같은 방법을 반복한다. 2D 함수에서 step1-3는 아래와 같이 작동한다.

Active Set Strategy

 GRG는 Equality Constraint만 고려한다. Active Set Strategy는 Inequality Constraint도 같이 고려하기 위한 방법으로 active한 Inequality constraint을 고려해 Optimization할 수 있다.

 initial working set을 임의로 설정해 feasible point를 초기값으로 선정한다. 그리고 Objectinve function값을 최소화시키는 방향으로 최적화를 진행한다. 이 값이 만약 새로운 Inequality constraint(g2)인 경우에는 working set에 g2를 넣고 다시 Optimization을 실시한다.

 만약 active constraint들의 Lagrange Multipliers가 0보다 작다면, 이는 Inactive Constraint을 의미한다고 볼 수 있다. 따라서 Active Constraint만 고려하는 Active Set Strategy의 Working set에서 제거한다.

 

Algorithm 구성

Step	Example	Algorithm
Step1	Set = g1, g2	초기 Working set을 가지고 시작한다.
Step2	Set = g1, g2	Working Set을 가지고 문제를 풀어본다..
Step3	constraints = g1,g2,g3,g4	모든 Constraints과 Lagrange Multipliers를 확인한다.
Step4	Satisfied and positive	모든 조건을 만족하고 Lagrange Multipliers가 0보다 크다면 중단한다.
Step5	LM = -1000(min) < 제거!	Lagrange Multipliers가 0보다 작다면, 가장 작은 LM을 찾아 Working Set에서 제외한다.
Step6	g3 불만족!	몇몇 제약조건에 위배된다면, 그 제약조건을 Working Set에 편입한다.
Step7	go to step 2	Step2로 돌아간다.

 

Barrier Method

Constraint Problem을 푸는 것 대신에, Barrier function으로 변환해 최적화를 진행하는 것도 고려해 볼 수 있다.

r > 0

여기서 B(x)가 Barrier function인데, Barrier Function은 크게 Logarithmic, Inverse 방식 등 두 가지 방식으로 식을 표현할 수 있다.

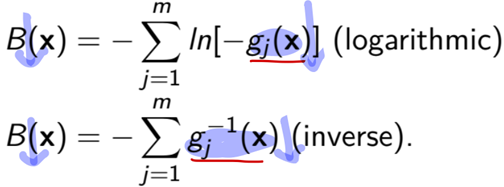
위 식은 $g_j(x)$가 작아지면, B(x)도 작아지는 함수다. 위 함수는 오로지 Inequality constraint에만 적용할 수 있다.

 

Algorithm

Step1 : Interior Point인 $x_0$를 찾는다. 점진적으로 감소할 수 있도록 함수를 설정한다. ${r_k} -> 0 for k -> infinite$ Set k = 0. ($r_k = 1/k$)

Step2 : k를 Iteration하면서 $T(x, r_k)$를 최소화한다. 이 때, Unconstrained method로 문제를 풀이한다. 

Step3 : 수렴여부를 판단한다. 만약 수렴하지 않는다면, k = k+1로 놓고 다시 step2로 돌아간다.

 

Penalty Function

Penalty function의 형태는 아래와 같다. 여기서 penalty function P(x)는 Quadratic Form으로 구성된다.

Inequality Constraint은 0과 비교해서 가장 큰 값을 뽑도록 한다. Equality Constraint은 그 자체로 곱해서 Penalty Function을 구성한다.

 

Barrier와 Penalty Function의 차이점

Penalty Function은 Constraint을 위반할 때 Penalty를 주어 Optimization이 되지 않도록 유도하는 방법이다. 그래서 패널티를 주었음에도 확연히 작은 값(최적값)을 가진다면, Infeasible Region에서도 값들을 뽑아낼 수 있다. 반면, Barrier Method는 절대 Feasible Region을 벗어나지 않는다.